Calcul de la déclinaison magnétique

Contexte : La topographieLa science de la représentation graphique et détaillée de la surface de la Terre..

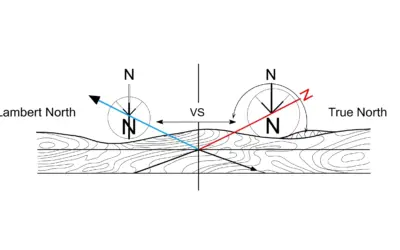
En topographie, l'orientation est cruciale. Les instruments comme la boussole indiquent le Nord Magnétique (NM)La direction indiquée par l'aiguille d'une boussole, qui pointe vers le pôle Nord magnétique., qui ne coïncide pas avec le Nord Géographique (NG)La direction du pôle Nord terrestre, un point fixe qui est l'axe de rotation de la Terre., la référence pour les cartes. L'angle entre ces deux directions est la déclinaison magnétique (Dm)L'angle horizontal entre le Nord géographique et le Nord magnétique en un point donné.. Comme le champ magnétique terrestre évolue, cette déclinaison change avec le temps. Un topographe doit donc savoir la calculer pour corriger ses mesures et garantir la précision de ses plans.

Remarque Pédagogique : Cet exercice vous apprendra à actualiser une déclinaison magnétique et à l'utiliser pour convertir un azimut magnétique en azimut géographique, une compétence fondamentale pour tout technicien du terrain.

Objectifs Pédagogiques

Comprendre la différence entre le Nord géographique et le Nord magnétique.
Savoir calculer la déclinaison magnétique pour une date spécifique à partir de données de référence.
Apprendre à corriger un azimut magnétique pour obtenir un azimut géographique.
Se familiariser avec la variation séculaire de la déclinaison.

Données de l'étude

Un topographe effectue un levé le 26 août 2025 à Hénin-Beaumont. Il utilise une carte topographique récente qui fournit les informations magnétiques suivantes.

Relation Angulaire : Nord, Déclinaison et Azimuts

Caractéristique	Valeur
Lieu du levé	Hénin-Beaumont, France
Date du levé	26 août 2025
Déclinaison de référence (1er jan. 2020)	+1° 12' E (Est)
Variation annuelle moyenne	+0° 8' (se déplace vers l'Est)
Azimut magnétique mesuré (Station → Point A)	112° 45'

Questions à traiter

Calculer l'intervalle de temps (en années décimales) entre la date de référence et la date du levé.
Calculer la variation totale de la déclinaison sur cette période.
Déterminer la déclinaison magnétique corrigée à la date du levé.
Calculer l'azimut géographique de la direction "Station → Point A".

Les bases sur la Déclinaison Magnétique

Pour orienter correctement un plan, toutes les mesures d'angle doivent être rapportées au Nord Géographique (NG), qui est une direction fixe. Cependant, une boussole indique le Nord Magnétique (NM), une direction variable. La correction de cette différence est une étape essentielle.

1. Définitions Clés

Nord Géographique (NG) : Direction du pôle Nord de rotation de la Terre. C'est la référence absolue et immuable pour les cartes.
Nord Magnétique (NM) : Direction indiquée par une boussole, influencée par le champ magnétique terrestre. Sa position varie dans le temps.
Déclinaison Magnétique (Dm) : Angle horizontal entre le NG et le NM. Elle est dite "Est" ou positive (+) si le NM est à l'Est du NG, et "Ouest" ou négative (-) si le NM est à l'Ouest du NG.

2. Formules de Correction
La déclinaison à une date donnée se calcule à partir d'une valeur de référence et de sa variation annuelle : \[ Dm_{\text{actuelle}} = Dm_{\text{référence}} + (\text{Variation annuelle} \times \Delta t) \] Où \( \Delta t \) est le temps écoulé en années. Pour corriger un azimut, on utilise : \[ Az_{\text{géographique}} = Az_{\text{magnétique}} + Dm_{\text{actuelle}} \]

Correction : Calcul de la Déclinaison Magnétique

Question 1 : Calculer l'intervalle de temps (en années décimales)

Principe

Le champ magnétique terrestre évolue constamment. Pour corriger une mesure, il faut savoir précisément combien de temps s'est écoulé depuis la dernière valeur de référence connue. C'est le principe de l'actualisation d'une donnée variable dans le temps.

Mini-Cours

La variation du champ magnétique terrestre est appelée variation séculaire. Elle n'est pas parfaitement linéaire, mais pour les calculs topographiques sur quelques décennies, on utilise un modèle linéaire simple : une variation annuelle moyenne. Pour des calculs de haute précision, les géophysiciens utilisent des modèles plus complexes comme l'IGRF (International Geomagnetic Reference Field).

Remarque Pédagogique

La clé ici est la précision. Ne vous contentez pas d'arrondir à l'année. Convertir la date exacte en une fraction d'année garantit que la correction sera juste. Pensez-y comme à un calcul d'intérêts : chaque jour compte.

Normes

Il n'y a pas de "norme" au sens réglementaire pour ce calcul, mais une convention universelle en sciences et en topographie : l'utilisation de l'année grégorienne et de ses subdivisions pour les calculs temporels.

Formule(s)

Formule de l'intervalle de temps

\Delta t = \text{Date}_{\text{levé}} - \text{Date}_{\text{référence}}

Formule de la date décimale

\text{Date}_{\text{décimale}} = \text{Année} + \frac{\text{Jour de l'année}}{\text{Jours totaux dans l'année}}

Hypothèses

Nous faisons l'hypothèse que la variation annuelle fournie est constante sur toute la période. C'est une simplification acceptable pour des durées de 5 à 10 ans.

Donnée(s)

Paramètre	Valeur
Date de référence	1er janvier 2020
Date du levé	26 août 2025

Astuces

Pour trouver rapidement le jour de l'année, vous pouvez utiliser un calendrier en ligne ou une petite fonction dans un tableur. Pour le 26 août, on peut aussi faire (nombre de mois pleins) + (jours du mois en cours). Par exemple, 7 mois pleins + 26 jours.

Schéma (Avant les calculs)

Frise Temporelle du Problème

Calcul(s)

Nous allons décomposer le calcul en deux étapes claires pour déterminer la durée exacte.

Calcul de la date du levé en format décimal

\begin{aligned} \text{Date}_{\text{levé}} &= 2025 + \frac{238}{365} \\ &\approx 2025,652 \end{aligned}

Calcul de l'intervalle de temps \( \Delta t \)

\begin{aligned} \Delta t &= \text{Date}_{\text{levé}} - \text{Date}_{\text{référence}} \\ &= 2025,652 - 2020,0 \\ &= 5,652 \text{ années} \end{aligned}

Schéma (Après les calculs)

Frise Temporelle avec Résultat

Réflexions

Le résultat de 5,652 années montre que plus de cinq ans et demi se sont écoulés. Ignorer la fraction d'année (0,652) aurait entraîné une erreur non négligeable dans la correction finale.

Points de vigilance

Attention aux années bissextiles ! Si la période de calcul enjambe une année bissextile (comme 2020 ou 2024), le nombre de jours dans cette année est de 366, ce qui change légèrement le calcul de la fraction décimale.

Points à retenir

La conversion des dates en format décimal est une technique de base pour tous les calculs impliquant des variations temporelles. Maîtrisez-la.

Le saviez-vous ?

Le pôle Nord magnétique se déplace actuellement de façon étonnamment rapide (environ 55 km par an) depuis le Canada en direction de la Sibérie, obligeant les scientifiques à mettre à jour les modèles magnétiques mondiaux plus fréquemment que par le passé.

FAQ

Résultat Final

L'intervalle de temps écoulé est d'environ 5,65 années.

A vous de jouer

Si le levé avait eu lieu le 1er juillet 2023, quel aurait été l'intervalle de temps \( \Delta t \) ? (1er juillet = 182ème jour)

Question 2 : Calculer la variation totale de la déclinaison

Principe

Le concept physique est l'extrapolation linéaire. En supposant que la vitesse de changement (la variation annuelle) est constante, on peut prédire le changement total sur une période donnée en multipliant simplement la vitesse par le temps.

Mini-Cours

Les angles en topographie sont exprimés en système sexagésimal (degrés, minutes, secondes). 1 degré (°) = 60 minutes ('). 1 minute (') = 60 secondes ("). Pour les calculs, il est souvent plus simple de convertir ces angles en degrés décimaux (ex: 1° 30' = 1,5°), d'effectuer les opérations, puis de reconvertir le résultat en format sexagésimal.

Remarque Pédagogique

Organisez bien vos calculs. Convertissez d'abord les unités angulaires en un format unique (degrés décimaux), faites la multiplication, puis reconvertissez à la fin. Cela évite les erreurs de calcul avec les minutes et les secondes.

Normes

Il n'y a pas de norme spécifique, mais la méthode de conversion entre degrés sexagésimaux et décimaux est une convention mathématique standard.

Formule(s)

Formule de la variation totale

\text{Variation}_{\text{totale}} = \text{Variation}_{\text{annuelle}} \times \Delta t

Hypothèses

On maintient l'hypothèse d'une variation linéaire et constante de +0° 8' par an sur toute la période considérée.

Donnée(s)

Paramètre	Symbole	Valeur	Unité
Intervalle de temps	\( \Delta t \)	5,652	années
Variation annuelle	-	+0° 8'	par an

Astuces

Pour convertir rapidement des minutes en degrés décimaux de tête, divisez par 60. Astuce : diviser par 60, c'est comme diviser par 6 puis par 10. Donc 8 / 6 ≈ 1,33, puis 1,33 / 10 = 0,133.

Schéma (Avant les calculs)

Visualisation de la Variation Annuelle

Calcul(s)

Pour trouver la variation totale, nous devons d'abord travailler avec des unités compatibles (degrés décimaux).

Conversion de la variation annuelle en degrés décimaux

\text{Variation}_{\text{annuelle}} = 0° + \frac{8'}{60} \approx +0,1333 \text{ °/an}

Calcul de la variation totale en degrés décimaux

\begin{aligned} \text{Variation}_{\text{totale}} &= \text{Variation}_{\text{annuelle}} \times \Delta t \\ &= 0,1333 \text{ °/an} \times 5,652 \text{ ans} \\ &\approx +0,7534° \end{aligned}

Reconversion en format sexagésimal

\begin{aligned} 0,7534° &= 0° + (0,7534 \times 60)' \\ &\approx 45,2' \\ &\Rightarrow \text{arrondi à } 0° 45' \end{aligned}

Schéma (Après les calculs)

Variation Totale sur la Période

Réflexions

Une variation de 45 minutes d'arc est considérable en topographie. Sur une distance de 1 km, une telle erreur d'angle provoquerait un écart de positionnement d'environ 13 mètres. Cela souligne l'importance de cette correction.

Points de vigilance

Le signe de la variation est crucial. Ici, c'est "+0° 8'", ce qui signifie que la déclinaison Est augmente. Si la variation était négative, la déclinaison se déplacerait vers l'Ouest (ou une déclinaison Est diminuerait).

Points à retenir

La multiplication d'un angle par un scalaire (le temps) se fait plus facilement en format décimal. C'est une méthode à retenir pour tous les calculs angulaires.

Le saviez-vous ?

Les navigateurs utilisaient autrefois des cartes de déclinaison (cartes isogoniques) qui montraient des lignes de même déclinaison pour corriger leur cap en mer. Ces cartes devaient être rééditées régulièrement.

FAQ

Résultat Final

La variation totale de la déclinaison sur la période est de +0° 45'.

A vous de jouer

Avec une variation annuelle de -0° 5' (vers l'Ouest) sur la même période de 5,652 ans, quelle serait la variation totale (en minutes arrondies) ?

Question 3 : Déterminer la déclinaison magnétique corrigée

Principe

Le principe est celui d'une mise à jour. On part d'une valeur connue à un instant T (la référence) et on lui applique le changement calculé pour obtenir la nouvelle valeur à l'instant T + Δt.

Mini-Cours

L'addition d'angles en format sexagésimal se fait colonne par colonne (secondes, minutes, degrés), de droite à gauche, comme une addition de nombres classiques. La seule différence est la "retenue" : si la somme des minutes dépasse 60, on soustrait 60 des minutes et on ajoute 1 aux degrés.

Remarque Pédagogique

Posez l'addition verticalement, en alignant bien les degrés sous les degrés et les minutes sous les minutes. C'est la meilleure façon de ne pas s'embrouiller et de bien gérer les retenues.

Normes

Pas de norme applicable, il s'agit d'une opération arithmétique de base.

Formule(s)

Formule de la déclinaison actualisée

Dm_{\text{actuelle}} = Dm_{\text{référence}} + \text{Variation totale}

Hypothèses

Nous supposons que les données initiales de la carte (Dm de référence et variation) sont exactes pour le lieu considéré.

Donnée(s)

Paramètre	Valeur
Déclinaison de référence (2020)	+1° 12' E
Variation totale calculée	+0° 45'

Schéma (Avant les calculs)

Composition des Angles de Déclinaison

Calcul(s)

Calcul de la déclinaison actualisée

\begin{aligned} Dm_{\text{2025}} &= Dm_{\text{2020}} + \text{Variation totale} \\ &= (+1° 12') + (+0° 45') \\ &= 1° 57' \text{ E} \end{aligned}

Schéma (Après les calculs)

Déclinaison Finale en 2025

Réflexions

La valeur a significativement augmenté, passant de 1,2° à près de 2°. Cela montre que même en quelques années, la correction peut devenir substantielle et ne doit jamais être négligée.

Points de vigilance

Attention à l'addition d'angles de signes différents. Si la déclinaison de référence avait été Ouest (-), on aurait eu : (-1° 12') + (+0° 45') = -0° 27', soit 0° 27' Ouest.

Points à retenir

L'actualisation d'une déclinaison est une addition algébrique simple : on respecte les signes (+ pour Est, - pour Ouest) de la valeur de départ et de la variation.

Le saviez-vous ?

La ligne de déclinaison nulle (où le Nord magnétique et géographique sont alignés) est appelée la "ligne agonique". Elle traverse actuellement l'Europe de l'Est.

FAQ

Résultat Final

La déclinaison magnétique à Hénin-Beaumont le 26 août 2025 est de +1° 57' E.

A vous de jouer

Si la Dm de référence était de 0° 10' Ouest (-0° 10') et la variation totale de +0° 45', quelle serait la Dm actuelle (en minutes) ?

Question 4 : Calculer l'azimut géographique

Principe

C'est l'objectif final du topographe : convertir une mesure de terrain (magnétique) en une mesure exploitable sur une carte (géographique). Le principe est de faire "pivoter" la référence de l'azimut, du Nord Magnétique vers le Nord Géographique, en appliquant la correction angulaire qu'est la déclinaison.

Mini-Cours

La relation fondamentale est : Azimut Géographique = Azimut Magnétique + Déclinaison Magnétique. Cette formule est la pierre angulaire de l'orientation en topographie. Il est utile de la visualiser (voir le schéma de l'énoncé) pour ne jamais se tromper de signe. Si la déclinaison est Est (+), l'azimut géographique sera plus grand que l'azimut magnétique.

Remarque Pédagogique

Toujours se faire un petit croquis mental ou sur papier. Dessinez le NG vertical, puis placez le NM à l'Est ou à l'Ouest selon le signe de la Dm. Placez ensuite votre direction (Azimut). Vous verrez immédiatement si vous devez ajouter ou soustraire l'angle.

Normes

Les plans topographiques et cadastraux officiels sont toujours orientés par rapport au Nord Géographique. C'est une obligation pour assurer la cohérence entre tous les documents cartographiques d'un territoire.

Formule(s)

Formule de l'azimut géographique

Az_{\text{géographique}} = Az_{\text{magnétique}} + Dm

Hypothèses

On suppose que la mesure de l'azimut magnétique n'a pas été perturbée par des anomalies magnétiques locales (présence de grosses masses métalliques, lignes à haute tension, gisements de fer...).

Donnée(s)

Paramètre	Valeur
Azimut magnétique mesuré (\(Az_{\text{m}}\))	112° 45'
Déclinaison actuelle (\(Dm\))	+1° 57'

Schéma (Avant les calculs)

Relation Angulaire à Résoudre

Calcul(s)

Le calcul final se fait en deux temps : une addition simple, suivie d'une normalisation du résultat pour respecter le format sexagésimal.

Addition de l'azimut magnétique et de la déclinaison

\begin{aligned} Az_{\text{géographique}} &= Az_{\text{magnétique}} + Dm \\ &= 112° 45' + 1° 57' \\ &= 113° 102' \end{aligned}

Normalisation des minutes

\begin{aligned} 102' &= 60' + 42' \\ &= 1° + 42' \end{aligned}

Calcul final de l'azimut géographique

\begin{aligned} Az_{\text{géographique}} &= 113° + 1° 42' \\ &= 114° 42' \end{aligned}

Schéma (Après les calculs)

Le schéma final montre la relation entre les directions avec les valeurs angulaires calculées, confirmant que l'azimut géographique est bien la somme de l'azimut magnétique et de la déclinaison Est.

Visualisation du Résultat Final

Réflexions

Le résultat final, 114° 42', est la direction qui devra être reportée sur le plan topographique officiel. L'écart de près de 2° avec la mesure de terrain est faible pour une visée courte, mais deviendrait une erreur de plusieurs dizaines de mètres sur un projet d'alignement routier ou de canalisation de plusieurs kilomètres.

Points de vigilance

L'erreur la plus commune est d'inverser le signe de la correction. Retenez : "De magnétique à géographique, on ajoute la déclinaison". Pour passer de géographique à magnétique (par exemple, pour s'orienter sur le terrain à partir d'une carte), on soustrait la déclinaison.

Points à retenir

La formule \( Az_{\text{géographique}} = Az_{\text{magnétique}} + Dm \) est à connaître par cœur. La maîtrise de l'addition d'angles sexagésimaux est indispensable.

Le saviez-vous ?

Les aéroports doivent régulièrement repeindre les numéros de leurs pistes, car ces numéros correspondent à leur orientation magnétique (par exemple, la piste 09 est orientée à 90°). Avec la variation séculaire, cette orientation change et les numéros doivent être mis à jour.

FAQ

Résultat Final

L'azimut géographique de la direction "Station → Point A" est de 114° 42'.

A vous de jouer

Si l'azimut magnétique était de 280° 30' et la déclinaison de -2° 40' (Ouest), quel serait l'azimut géographique ?

Outil Interactif : Simulateur de Déclinaison

Utilisez le curseur ci-dessous pour voir comment la déclinaison magnétique à Hénin-Beaumont évolue dans le temps, sur la base des données de l'exercice. Observez comment la valeur change sur le graphique.

Paramètres d'Entrée

Année du calcul 2025

Résultats Clés

Déclinaison Calculée -

Quiz Final : Testez vos connaissances

1. Qu'est-ce que la déclinaison magnétique ?

L'angle vertical entre la boussole et le sol.
L'angle horizontal entre le Nord géographique et le Nord magnétique.
La variation de l'altitude d'un point.

2. Si la déclinaison est de 2° Est et l'azimut magnétique de 100°, quel est l'azimut géographique ?

102°
98°
100°

3. Que se passe-t-il si on ignore la déclinaison magnétique pour un projet de grande envergure ?

Rien, la différence est négligeable.
Les mesures d'altitude seront fausses.
Le projet sera mal orienté par rapport aux limites de propriété et aux autres infrastructures.

Azimut: Angle horizontal mesuré dans le sens des aiguilles d'une montre à partir d'une direction de référence (généralement le Nord).
Déclinaison Magnétique: L'angle au niveau d'un point à la surface de la Terre entre le Nord géographique (direction du pôle Nord) et le Nord magnétique (direction indiquée par une boussole).
Nord Géographique (NG): Aussi appelé "Nord vrai", c'est la direction du pôle Nord, qui est un point fixe sur le globe terrestre.
Nord Magnétique (NM): La direction vers laquelle pointe l'aiguille d'une boussole. Ce point se déplace au fil du temps en raison des changements dans le noyau terrestre.